Біурок з літератури та математики за мотивами оповідання Майка Гелпріна «Свіча горіла на столі, свіча горіла…» (10 клас)

 

 

 

Людмила Федорова – вчитель літератури

Віктор Ловінський – вчитель математики

 

Біурок з літератури та математики за мотивами оповідання Майка Гелпріна «Свіча горіла на столі, свіча горіла…» (10 клас)

Тема. Трансцендентність людини.

Мета: розкрити філософський зміст оповідання; розвивати уміння знаходити спільне в різних об’єктах та поєднувати їх в єдине; виховувати любов до поезії та математики.

 

 

Хід уроку

І. Робота з епіграфом як лемою до розкриття трансцендентності людини

Література

Аналіз організаційної діаграми – евристична бесіда:

 

 

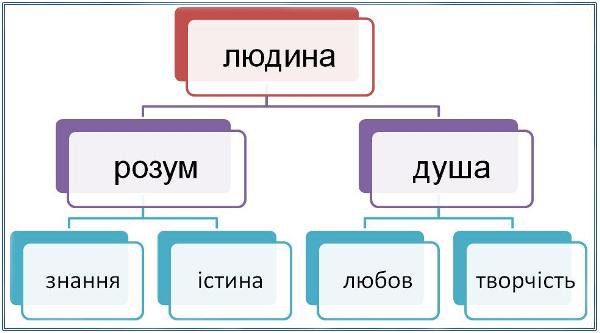
Питання бесіди з гіперпосиланнями:

–        Що таке людина?

–         Розум і душа – філософські категорії та складові людини.

–         Де «розміщені» розум, а де – душа в людини?

–         Що об’єднує/роз’єднує розум і душу?

 

Схема бесіди:

 

 

 

 

Математика

Аналіз організаційної діаграми – евристична бесіда:

 

 

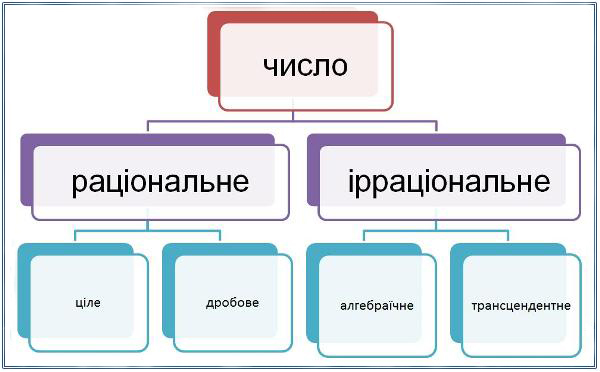
Питання бесіди з гіперпосиланнями:

 

–      Що таке число?

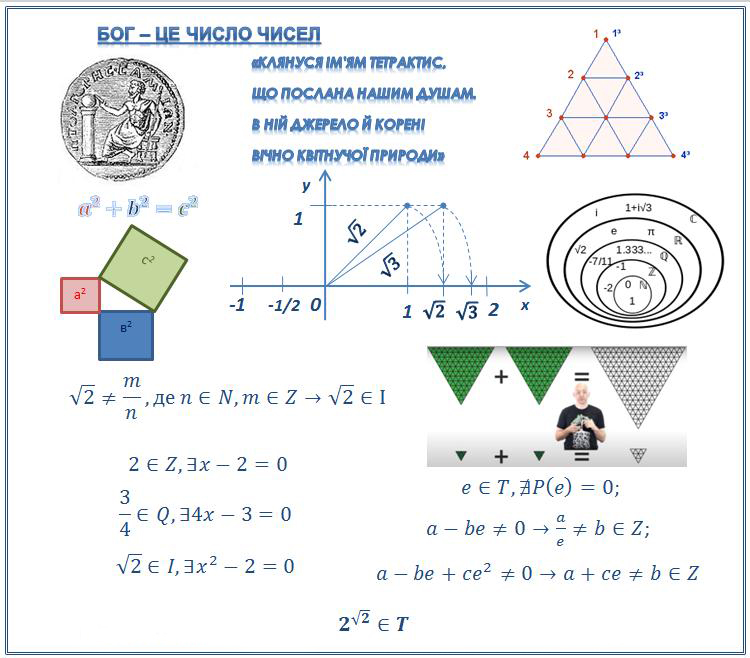
–        Число у піфагорійців.

–        Геометрична інтерпретація чисел.

–       Теорема, яка призвела до проблеми неспівмірності відрізків.

–        Зображення чисел на числовій площині.

–        Різниця між раціональними та ірраціональними числами.

–        Різниця між алгебраїчними і трансцендентними числами.

–        Як за допомогою  отримати трансцендентне число.

 

Схема бесіди:

 

 

 

ІІ. Трансцендентність – ознака людини?

 

Література

Питання бесіди з гіперпосиланнями

– Що таке трансцендентність?

– Що таке комп’ютерна симуляція?

– Що трансцендентного у симуляції ДРГ-439К?

– Що таке симбіоз?

– Що є витвором симбіозу людського мозку та душі?

– Що таке екстаз?

– Які твори музики, поезії, живопису чи інших творінь людини (математики, комп’ютерних ігор) викликають захоплення?

 

 

Математика

• Заперечення математиками моделювання комп’ютерної симуляції.

Для зберігання матриці, що описує поведінку 20 спінів квантових часток, знадобиться терабайт ОСУ. Екстраполювавши ці дані всього на декілька сотень спінів, ми отримаємо, що для створення комп’ютера з таким об’ємом пам’яті знадобиться більше атомів, ніж їх загальна кількість у Всесвіті. Зростання все можливої кількості варіантів відбувається за експоненціальним законом.

 

 

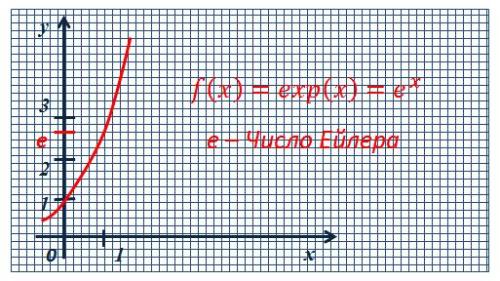
               Виникнення числа e.

 

Задача. Ви кладете на депозит у банку 1 гривню під 100 % річних, причому відсоток нараховується в кінці року. У результаті ви отримаєте 2 гривні. А яку суму ви отримаєте, якщо відсотки нараховуватимуть протягом року періодично (наприклад, двічі на рік, щокварталу, щомісяця, щотижня, щодня тощо) і докладатимуть нараховані відсотки до депозиту?

Розв'язання. Використовуючи формулу для складних відсотків, у кінці року з нарахуваннями за півріччя, будемо мати (1 + ½)² = 2,25 грн.

Якщо нарахування відсотків буде здійснюватись щоквартально, то в кінці року матимемо відповідно  (1 + ¼)⁴ ≈ 2,44 грн.  

При щомісячному нарахуванні –  (1 + 1/12)¹² ≈ 2,61 грн.

Щотижневому –  (1 + 1/52)⁵² ≈ 2,69 грн.

Щоденному –  (1 + 1/365)³⁶⁵ ≈ 2,71 грн.

Для довільного n кінцева сума буде обчислюватись:  (1 + 1/n)ⁿ .

Тоді,  

                                         

 

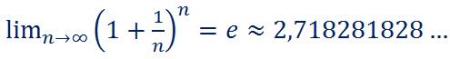
• Доведення трансцендентності числа  π .

Скористаємось тотожністю Ейлера  е^іπ = –1.

Якщо припустити, що π  – алгебраїчне,

а фактом є  e^{ірраціональне} = трансцендентне​,

то протиріччя з тотожністю (е^іπ дорівнює алгебраїчне),

доводить, що  π – трансцендентне.

 

• Цікаві обчислення:

 

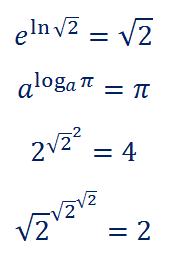
ІІІ. Завдання

Поміркуй:

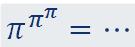• , можливо ціле?
• Чи можлива симуляція трансцендентності?

 

Матеріали люб'язно надано авторами – Людмилою Федоровою та Віктором Ловінським – спеціально для читачів "Малої Сторінки".

 

 

Завантажити урок у форматі doc.zip

 

 

Дивіться також на "Малій Сторінці":