Біурок з літератури та математики у 8 класі (2 год.)
Вчителі: Людмила Федорова та Віктор Ловінський
Тема: Філософські аспекти поетичної і математичної спадщини Омара Хайяма.
Мета: навчити учнів знаходити в творах Омара Хайяма актуальність порушених ним проблем; розвивати логічне та абстрактне мислення; виховати інтерес до творчої спадщини філософа.
Оформлення та обладнання класу: мультимедійне обладнання.
|
|
"Я тільки й знаю, що знання шукаю,
|
Зміст уроку
I. Пролог (під тиху східну мелодію)
Вчитель літератури
 В одній медресе́ навчалося троє юнаків. В стінах школи вони потоваришували і, як годиться справжнім друзям, дали один одному клятву: той, хто першим доб’ється успіху в житті, допоможе іншим. Ніхто з них тоді не знав, що один з друзів стане візиром, другий очолить релігійну секту, а третій прославиться як великий вчений і поет. Це були Нізам аль Мулк, Хасан ас-Саббах і Омар Хайям.
В одній медресе́ навчалося троє юнаків. В стінах школи вони потоваришували і, як годиться справжнім друзям, дали один одному клятву: той, хто першим доб’ється успіху в житті, допоможе іншим. Ніхто з них тоді не знав, що один з друзів стане візиром, другий очолить релігійну секту, а третій прославиться як великий вчений і поет. Це були Нізам аль Мулк, Хасан ас-Саббах і Омар Хайям.
 Першим добився успіху Нізам. Він став візиром сельджукського султана Малик-шаха, який правив у Персії. Пам’ятаючи клятву, він допоміг друзям. Хасану він дав місце при дворі. Але з часом він поїхав в Єгипет, де став послідовником ісмаїлітів (релігійної течії в ісламі). Омара, якого не цікавили високі пости і багатство, він забезпечив належними засобами, щоб той міг безбідно жити в рідному місті, займатися науками і писати рубаї.
Першим добився успіху Нізам. Він став візиром сельджукського султана Малик-шаха, який правив у Персії. Пам’ятаючи клятву, він допоміг друзям. Хасану він дав місце при дворі. Але з часом він поїхав в Єгипет, де став послідовником ісмаїлітів (релігійної течії в ісламі). Омара, якого не цікавили високі пости і багатство, він забезпечив належними засобами, щоб той міг безбідно жити в рідному місті, займатися науками і писати рубаї.
II. Оголошення теми, мети, структури уроку
III. Енциклопедична пауза
Вчитель математики
Філософські концепції – ідеї і думки про людське буття.
Свої філософські погляди на буття Омар Хайям виклав у «Трактаті про буття і повинність», написаному в 1080 році. Трактат був написаний у відповідь на лист імама та судді ан-Насаві, який пропонував «царю філософів Заходу і Сходу Абу-ль-Фатгу ібн Ібрагіму Хайяму» висловитися в питаннях «про мудрість творця у створенні світу й особливо людини, і про необхідність людям молитися». В праці можна знайти «відповідь на три питання: необхідність протиріч у світі, детермінізму та довговічності».
Вчитель за слайдом коротко роз’яснює світосприймання Омара Хайяма.

Спробуємо побачити в спадщині Омара Хайяма його філософські позиції.
IV. Літературна сторінка
Вчитель літератури
 В літературі Омар Хайям відомий завдяки своїм рубаї. Через велику кількість метафор, використаних автором, його твори важкі для перекладу. Деякі навіть стверджують, що Хайям засуджував Аллаха, не вірив у справедливість життя, був п’яницею та розбишакою, адже писав про вино і любов до жінок. Насправді, це спекуляція над перекладами. Просто автор використовував образи, порівняння та вкладав у зміст тонкий підтекст. Насправді він був глибоко духовною та мудрою людиною, вірив у Бога, що підтверджують всі поважні дослідники творчості Хайяма. Наприклад, Чарльз Хортон у передмові до «Рубайят», випущеного у Лондоні 1917 року, писав:
В літературі Омар Хайям відомий завдяки своїм рубаї. Через велику кількість метафор, використаних автором, його твори важкі для перекладу. Деякі навіть стверджують, що Хайям засуджував Аллаха, не вірив у справедливість життя, був п’яницею та розбишакою, адже писав про вино і любов до жінок. Насправді, це спекуляція над перекладами. Просто автор використовував образи, порівняння та вкладав у зміст тонкий підтекст. Насправді він був глибоко духовною та мудрою людиною, вірив у Бога, що підтверджують всі поважні дослідники творчості Хайяма. Наприклад, Чарльз Хортон у передмові до «Рубайят», випущеного у Лондоні 1917 року, писав:
«У Персії нема суперечок щодо віршів Омара і їх значення: автор шанується як великий релігійний поет. Його возвеличення вина і любові представляють собою класичні суфійські метафори: під вином розуміється духовна радість, а любов – радісна вірність Богу... Омар не виставляв свої знання напоказ, а камуфлював їх. Абсурдно відноситися до подібної людини як до п’яниці та нероби, однак його глибокі вірші, які здаються на перший погляд поверхневими, вводять в оману.»
|
|
Юначе, підведись — горить зоря ясна! В прозорі келихи налий вогню-вина! В цім тліннім закутку живеш ти мить… а потім, Хоч як жадатимеш, не вернеться вона. |
|
Сергій Маршак так відізвався про поета:
|
|
Четыре строчки источают яд, Когда живёт в них злая эпиграмма, Но раны сердца лечит Рубайят – Четверостишия старого Хайяма. |
|
Авторський переклад:
|
|
Чотири стрічки випускають яд, Коли живе в них жовчна епіграма, Та рани серця лічить Рубайят – Чотиривірш мудрого Хайяма. |
|
VI. Протиріччя – необхідна умова розвитку
Вчитель літератури
Учні читають рубаї і знаходять в них філософський зміст, що пояснює «необхідність протиріч».
|
|
Джерело ми розваги і смутку копна, Ми – сонце щастя й горя океан. Коли ліпив Творець моє єство із глини Якщо Творцю неприйнятні мої бажання, |
|
Вчитель математики
Ми вже маємо поняття про числа: натуральні, цілі, раціональні, ірраціональні, дійсні. Ірраціональні числа √2, π = 3,1415926… - нескінченні десяткові дроби.
Зобразимо відрізок довжиною √2.
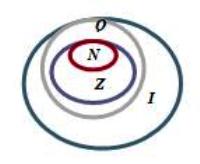
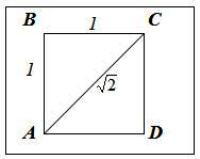
Чи можна зобразити нескінченне число скінченною довжиною відрізка?
Це протиріччя між геометрією і алгеброю, що прийшло з древньої Греції, успішно вирішив О. Хайям задовго до Декарта, Ньютона та Кантора. На відміну від Евкліда та інших давньогрецьких математиків, Омар Хайям не тільки не протиставляв числа неперервним величинам, геометрію — арифметиці, а й намітив конкретні шляхи до виявлення єдності протилежностей, до ліквідації прірви між дискретністю та неперервністю.
Вчений підійшов до цього протиріччя філософськи і створив новий вид чисел – ірраціональні.
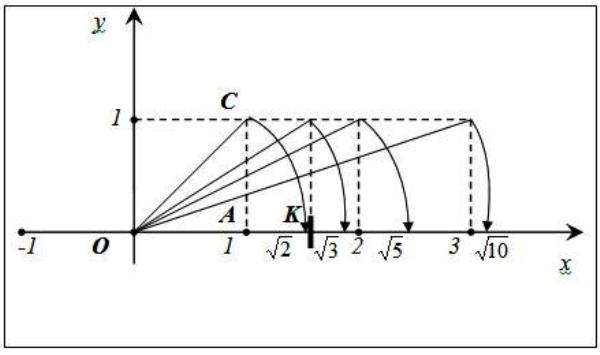
Їх можна зображати на числовій осі точками. Нехай дано числову вісь з початковою (нульовою) точкою О і одиничним відрізком ОА. Зобразимо на цій осі точку, що відповідає ірраціональному числу √2. Для цього будуємо на відрізку ОА = 1 квадрат, його діагональ ОС = √2. Якщо розхилом циркуля ОС провести дугу до перетину її з віссю. Одержана точка К і буде відповідати числу √2. Аналогічно отримуються: √3, √5, √10.
Кожному дійсному числу на числовій осі відповідає єдина точка. Навпаки, кожній точці на числовій осі відповідає єдине число. Кажуть, що між множиною точок числової осі і множиною дійсних чисел існує взаємно однозначна відповідність.
Але між множиною точок числової осі та множиною раціональних чисел не існує взаємно однозначної відповідності, оскільки не кожній точці осі відповідає раціональне число.
В математичній праці «Труднощі в арифметиці» Хайям розглядає метод знаходження коренів будь-якого показника з цілих чисел. В основі цього методу лежала формула, що пізніше одержала назву бінома Ньютона. Цей трактат не знайдений, але його згадував сам Хайям у «Трактаті про доведення задач алгебри та алмукабали».
Представимо підкореневий вираз у вигляді:
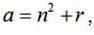
де n, r – натуральні числа.
Перетворимо праву частину на квадрат двочлена:
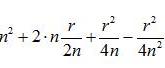
Знехтуємо дробом 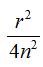 , як незначним відхиленням, отримаємо:
, як незначним відхиленням, отримаємо:
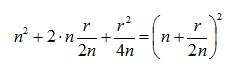
Таким чином:
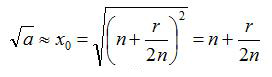
Застосуємо ітеративний (багаторазове повторення) процес уточнення.

Ітерації в цьому методі дуже швидко сходяться до √a, тобто майже не відрізняють від значення кореня.

В Європі цей метод почали використовувати значно пізніше.
Якщо так підходити до знаходження кореня кубічного, то при піднесенні до кубу бінома (х0 - х1) можна отримати розклад в ряд, з яким ви вже знайомі:
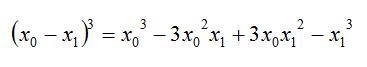
Складемо таблицю біноміальних коефіцієнтів для п = 5 у формі трикутника:
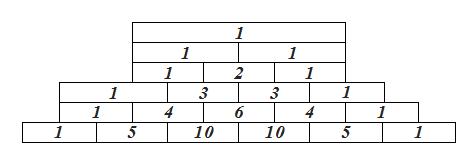
Сьогодні ця таблиця носить назву трикутник Паскаля.
VII. Детермінізм – всеосяжна причинність
Вчитель літератури
Детермінізмом пронизана вся творчість Хайяма. Цей принцип можна побачити в будь-якому рубаї. Чому? Бо він лежить в основі Всесвіту. Все, що відбувається має причину. Одні передумови породжують певну дію, а та, в свою чергу стає передумовою для наступної.
Читання найбільш співзвучних рубаїв і аналіз їх змісту.
|
|
I юних, і старих – всіх поглинає час, Що ти вартий на світі без волі небес? У колисці – дитина, покійник – в труні. Про вчора не гадай — воно навік зів’яло, |
|
Вчитель математики
Математики запозичили у філософів детермінант для означення свого поняття – визначник. (Детермінант – це число, яке отримується при обчисленні виразу за певним законом). Сьогодні ми проаналізуємо причинну наслідковість в теорії відношень і вченні про число. Друга та третя книги Омара Хайяма «Трактату про тлумачення темних положень у Евкліда» присвячені теорії відношень. Базуючись на Аристотелевій точці зору, він так сформулював принцип неперервності: «Величини можна ділити нескінченно, тобто вони не складаються з неподільних величин». Разом з тим, він пішов далі та ввів нове визначення пропорції, в якому рівність відношень зводилась до збігу їхнього розкладання на неперервні дроби. Він довів еквівалентність своєї теорії відношень з теорією Евкліда, пов’язав вже дві дійсні теорії (відношень чисел та загальної теорії відношень), та, базуючись на принципі неперервності, встановив при цьому існування загальної теореми про існування четвертої пропорційної до трьох даних величин. У третій книзі Хайям звернувся до множення відношень і саме тут по-новому трактував зв’язок понять відношення і числа. Він висловився за введення в математику подільної одиниці та нового роду чисел, за допомогою яких можна було б виразити будь-які відношення величин.
Знаходження четвертої пропорційної величини до трьох даних
На уроках геометрії ми навчилися будувати четвертий пропорційний відрізок з використанням узагальненої теореми Фалеса. Використаємо це у наступній задачі.
Задача. Знайти відношення:
- варіант 1 – площі квадрата до його діагоналі;
- варіант 2 – площі прямокутника до його діагоналі.
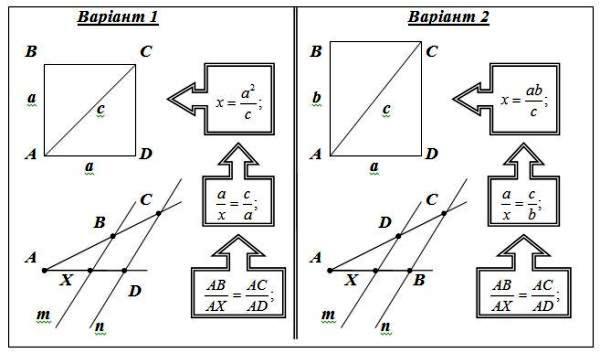
VIII. Довговічність – проблема актуальності, часу і еволюції
Вчитель літератури
Що життя коротке, а час швидкоплинний, що треба жити сьогоднішнім днем, радіти кожній миті – можна прочитати в переважній більшості рубаїв. Але при цьому, Омар Хайям закликає бути людей добрими, чесними, не вихвалятися своїми багатствами та знаннями. Закликає цінувати одвічне, що має справжню значимість для кожної людини, що стоїть поза часом.
|
|
Ти до зла не хились, а роби лиш добро! Марнославцем, для влади придатним, не будь. Не годиться вдаватись до лайки й образ, Йди з добром до людей – і воздасться тобі. |
|
IX. Самостійна робота
Літератори
Заповнюють радіальну діаграму «Філософські питання, які турбували поета»
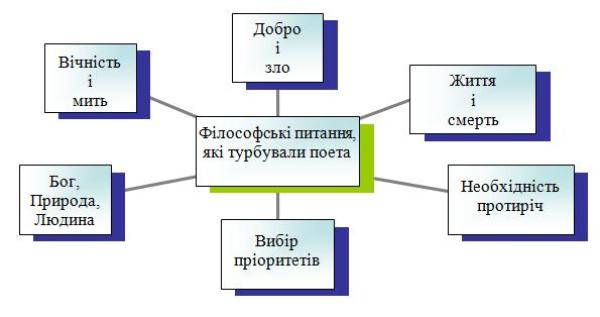
Математики
Знаходять значення √2, застосувавши триразову ітерацію.
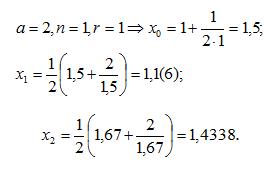
X. Домашнє завдання
Література – знайти у творчості поета пояснення трьох філософських понять: необхідність протиріч у світі, пріоритетів та довговічності.
Математика – обчислити √10 - √7.
Завантажити урок у форматі doc.zip
Дивіться також на "Малій Сторінці":


